Physics 510

Solution to problem 1.1

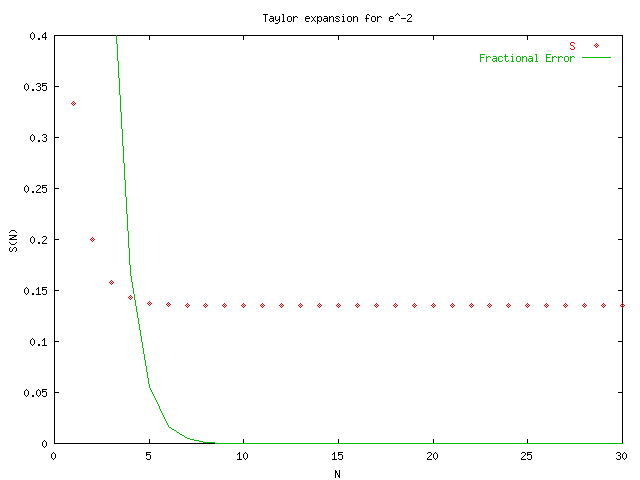
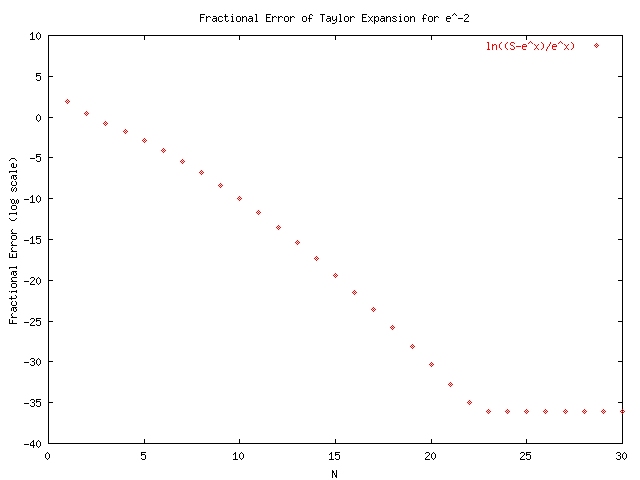
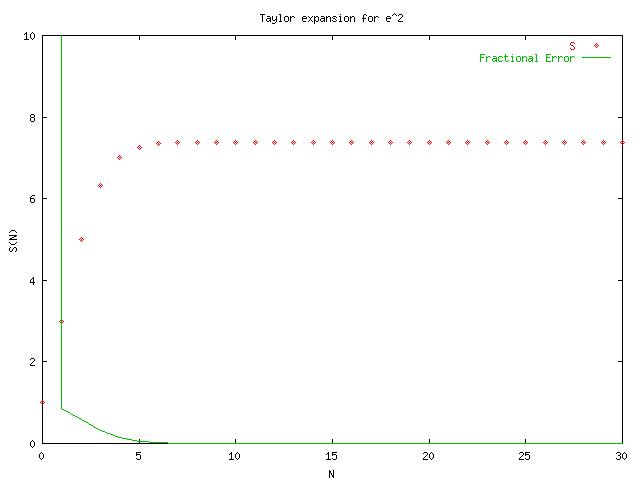
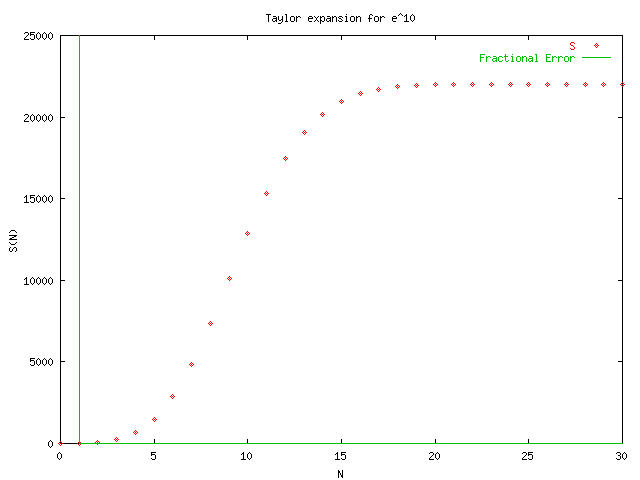
GNUplot was used to produce the following graphs by using the output of taylors_original.cpp and taylorsplot_original.txt.  From the graphs we see that the alternating series converges much slower than those for positive x.  This will lead to problems with the precision of the final sum which may loose significant digits when very large numbers are added and subtracted far away from the actual solution.  The function in taylors.cpp that is used to calculate S(x,N) is:

double S(const double x, const int N)
{
    double s=1;
    double f=1;

    for (int i=1;i<=N;i++)
    {
        f *= (x/i);
        s += f;
    };

    return s;
};

Notice a running sum is kept in order to increase efficiency.  After examining the plots and the series for e^-x it was evident that we would be better off using the identity e^-x = 1/e^x  ~= 1/S(x,N).  So the function was changed to:

double S(const double x, const int N)
{
    double s=1;
    double f=1;
    double inverse=0;

    if (x<0) inverse=1;

    for (int i=1;i<=N;i++)
    {
        f *= fabs(x/i);
        s += f;
    };
    if (inverse) s = 1/s;
    return s;
};

The difference in these two procedures can be seen by examining the last four plots which make use of this function for x<0.

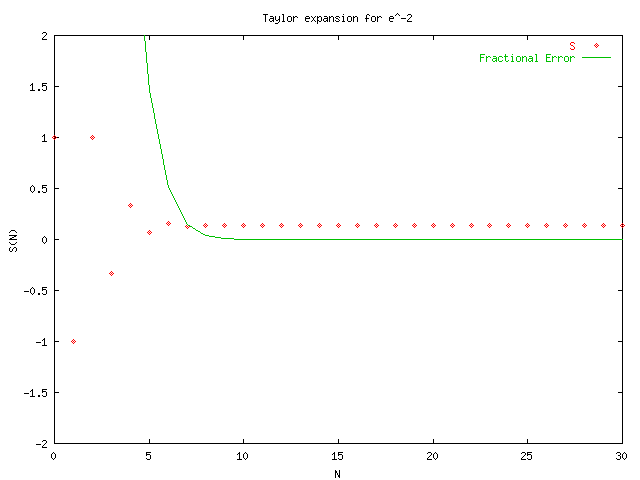
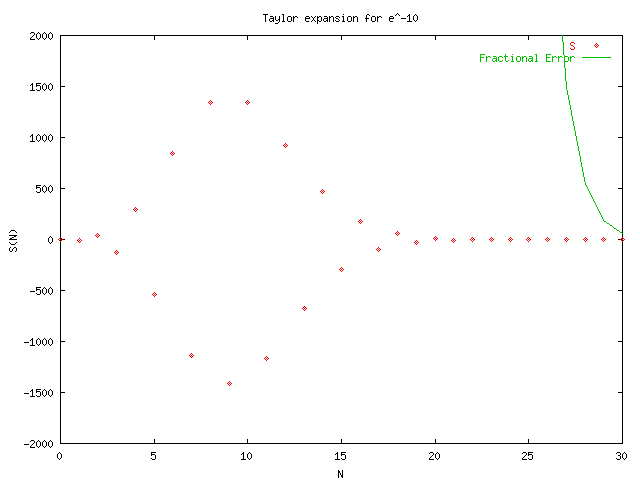
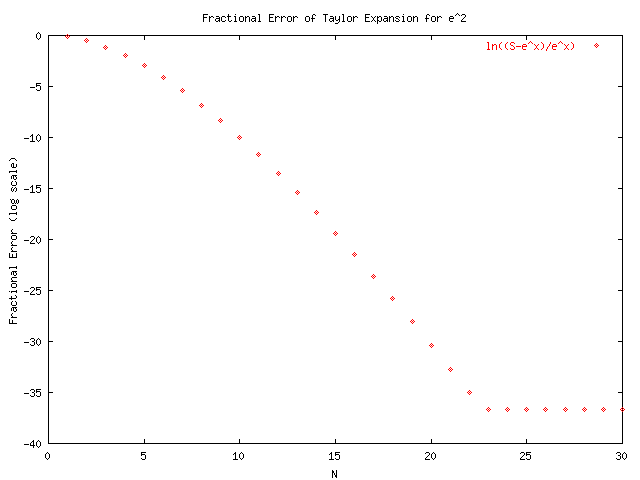
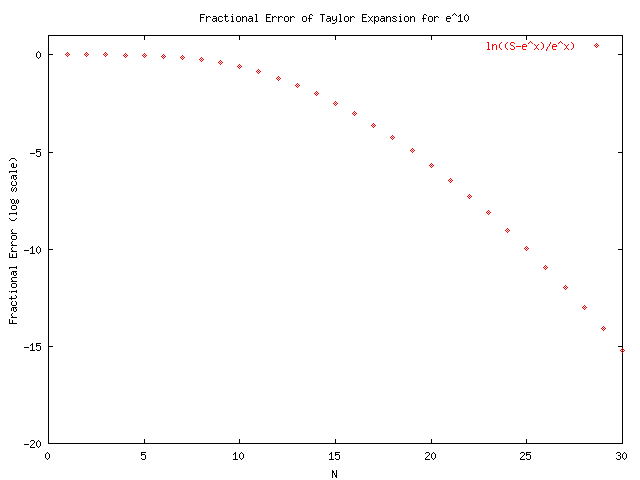
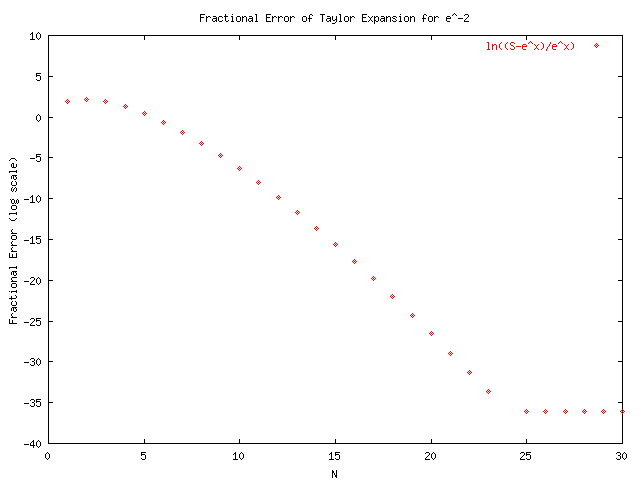
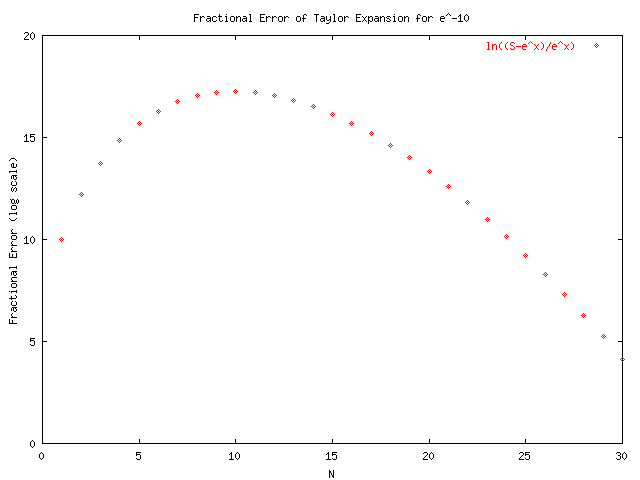
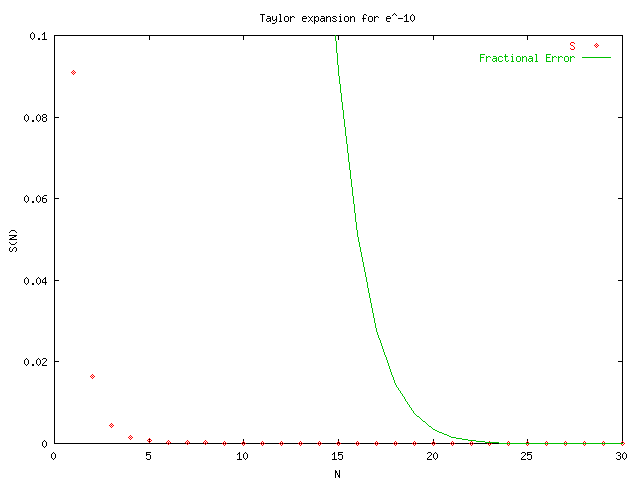
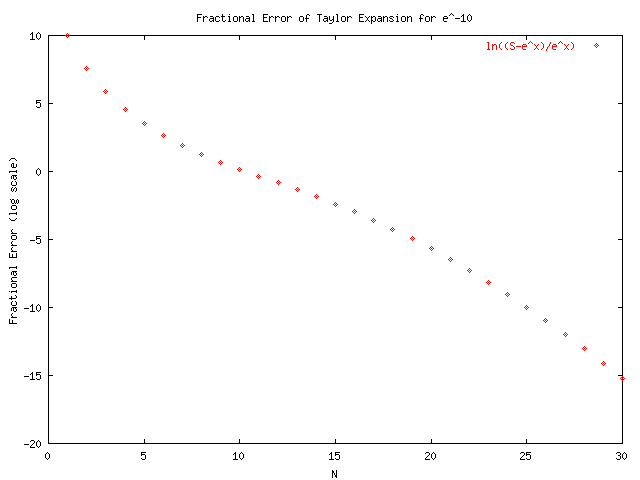
The following are the results after modifying function to use the identity e^-x = 1/S(x,N) as shown in taylors.cpp.txt.  A change in axis was needed as shown in taylorsplot.txt.

: