Answer for Assignment 6.13, 6.15, Paul Devries, A First Course in Computational Physics

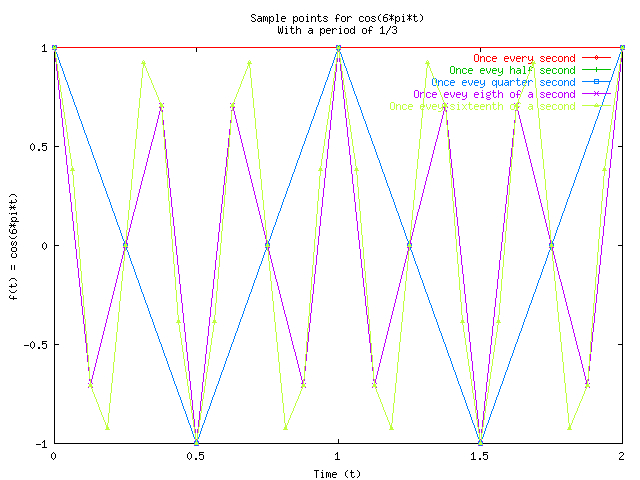
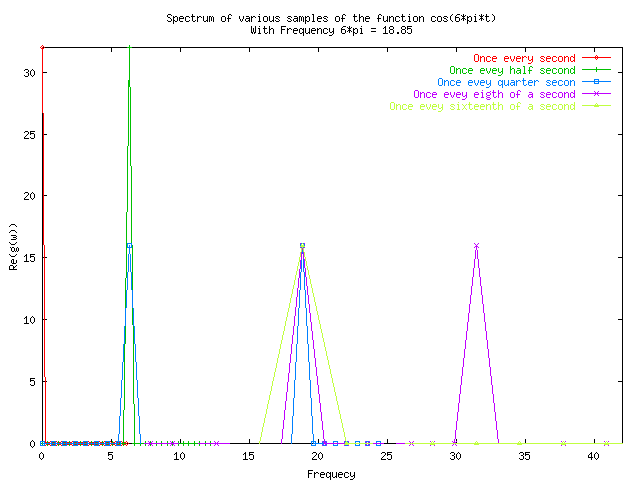
In order to examine the nature of the Fast Fourier Transform algorithm, originally developed by Cooper, we examine two functions f(t)= cos6¶t and cos3t. Seeing that the period of the function f(t) = cos6¶t has a period of 1/3,  the frequency is given by 2*pi divided by the period.  So the frequency should be plotted as a dirac delta function centered at 6*pi. 

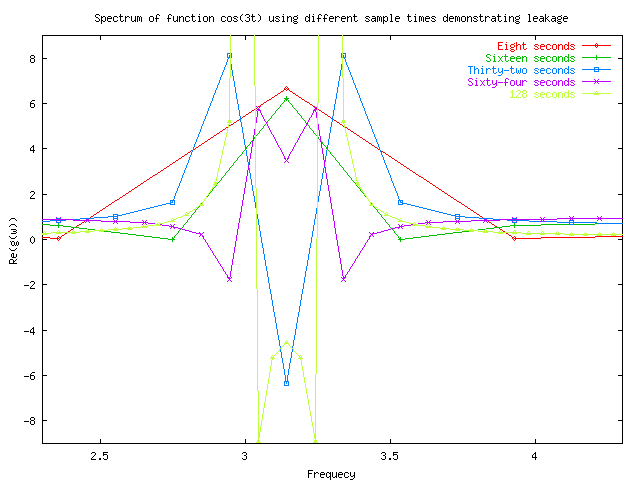
In order to demonstrate the flaws of Fast Fourier Transform with respect to undersampling and aliasing and leakage,  the following graphs were obtained using the code given in fft.cpp with dependency Funtion.h, using four11plot.txt, four11plot2.txt and four11plot4.txt to plot the output four11.txt.

For the function cos3t we can demonstrate the effect of leakage within the algorithm.  In the following graph we sample every second for 16, 32, and 64 seconds.  Because the sample rate is not commensurate with the period of the function, the frequency is represented by alternative frequencies close to the actual one, and averaged around it.