Answer for Assignment 10

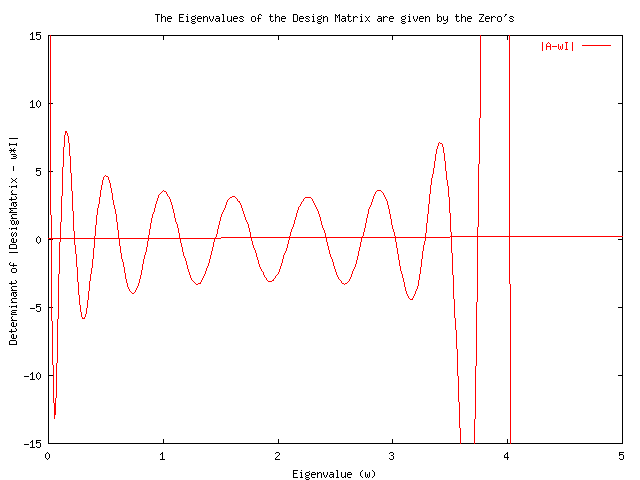
1. The matrix form of the Finite Difference Equation was constructed and it's eigenvalues were evaluated by finding the zeros of the graph of the constructed matrix (the design matrix) of the characteristic equation det|A-wI| = 0.  After examining the graph it became evident that the Bisection method was best suited for speedy calculations.  The determinant was evaluated by taking advantage of the Tridiagonal nature of the Matrix which allows for computation through the recurrence relation 

Dj = A[j,j]*D(j-1)-A[j-1,j]*A[j,j-1]*D(j-2).  where D= determinant of a jxj matrix and A= the design matrix.

This was implemented by overloading the virtual function det() in the Matrix derived class TridiangonalMatrix. The graph is given below and the first three eigenvalues were evaluated to be 

# e0 = 0.025733709335327
# e1 = 0.10294966697693
# e2 = 0.22951259613037

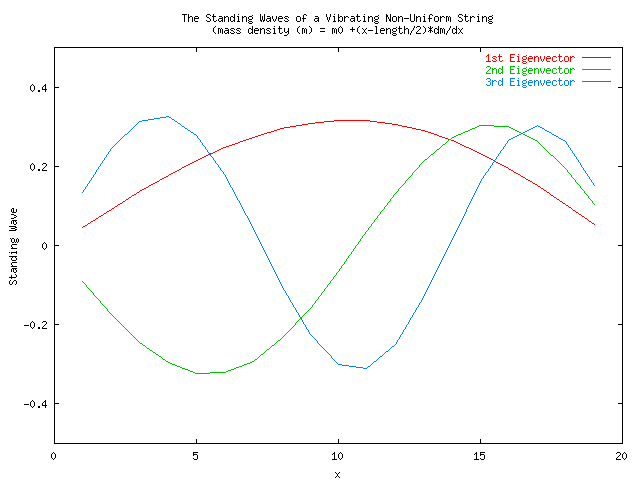
2. A C++ class was built expanding on Assignment 9. This allowed for the use of a convenient sort function after evaluating the eigenvalues using a QR algorithm. Finally,  LU decomposition algorithms were used to evaluate the eigenvectors using the inverse iteration method.