Answer for Assignment 4

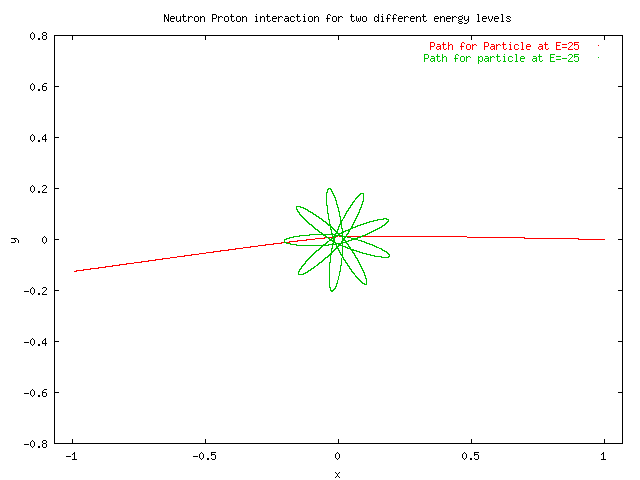
Below is the graph of the orbit of the conservative central force problem where U(r)=-ke^-r/a.  These paths were plotted using a Simpson numerical integral approximation to evaluate theta by performing a preservation of angular momentum derived formula giving an equation for theta in terms of an integral from an initial radius to the radius for which one wishes to determine theta.  

simpsons.cpp

#include <functional>
#include <iostream>
#include <math.h>

using namespace std;

const double pi = acos(-1);

class Function : public unary_function<double,double>
{
public:
	Function() {};
	virtual result_type operator()(argument_type x){return x;};
	virtual Function& getDerivative() { return *this;};
};

class ProtonNeutronFunc : public Function
{
public:
	ProtonNeutronFunc(double factor, double exponent_factor,  double angular, double energy) 
		:k(factor), a(exponent_factor), m(angular), E(energy)
	{};

	virtual result_type operator()(argument_type x)
	{
		return -1*k*exp(-1*x/a) + m/pow(x,2) - E;
	};

protected:
	double k;
	double a;
	double m;
	double E;

};

class ThetaOfR : public ProtonNeutronFunc
{
public:
	ThetaOfR(double factor, double exponent_factor,  double angular, double energy) 
		: ProtonNeutronFunc(factor, exponent_factor, angular, energy) 
	{};
	virtual result_type operator()(argument_type x)
	{
		return 2*m / ((x*x)*sqrt(4*m*( 0-ProtonNeutronFunc::operator ()(x) ) ) );
	};
};

class Approximation
{
public:
	Approximation(double lowerBound, double upperBound, Function& function)
		:a(lowerBound), b(upperBound), f(function)
	{};

	virtual double calculate(double precision, int maxTries = 3000)
	{
		cout << "Default approximation not implemented" << endl;
		return -1;
	}

protected:
	double a;
	double b;
	Function& f;
};

class SimpsonsApproximation : public Approximation

{
public:
	SimpsonsApproximation(double lowerBound, double upperBound, Function & function)	
		: Approximation(lowerBound, upperBound,function)
	{
		if (a >=b) cerr << "Lowerbound " << a << " is greater than or equal to upper bound " << b << endl;
	};

	virtual double calculate(double precision, int maxTries=50)
	{
		double i, sum0;
		double h = (b-a)/3;
		double se= f(a+2*h), so = f(a+h) + f(b-h), sd = f(a) + f(b);
		double sum = h*(sd + 2*se + 4*so)/3;
		if (h <= 0) return 0;
		do 
		{
			h/=2;
			sum0 = sum;
			se+=so;
			so =0;
			for (i = a+h; i < b; i+=2*h)
				so+=f(i);
			sum =  h*(sd  + 2*se +4*so)/3;
			//cout << sd << "\t" << se << "\t" << so << "\t" << sum << endl;
		}  while ((fabs((sum - sum0)/sum0) > precision) && (maxTries--));
		return sum;
	}
};

int main(int argc, char* argv[])
{
	ThetaOfR func25(70, 0.2, 0.01, 25);
	ThetaOfR funcneg25(70, 0.2, 0.01, -25);

	double r = 0, rmin=0.010458;
	double theta, thetaN;

	cout.precision(16);
	cout << "# Welcome to the Simpson numerical integral approximation program for the Neutron-Proton Derivative" << endl;
	cout << "# for E=25 theta(r) = " << endl;

	
	SimpsonsApproximation total25(rmin, 1, func25);
	thetaN=total25.calculate(0.0001);

	for (r=1;r >=rmin;r-=0.001)//*log(r/rmin))
	{
		SimpsonsApproximation sp(r, 1, func25);
		theta = sp.calculate(0.00001);
		cout << r*cos(theta) << "\t" << r*sin(theta) <<endl;
		cout << r*cos(2*thetaN - theta) << "\t" << r*sin(2*thetaN - theta) << endl;
	}

	cout << endl << "# for E=-25" << endl;

	SimpsonsApproximation totalneg25(0.0158798, 0.204010, funcneg25);
	thetaN=totalneg25.calculate(0.00001);

	for (r=0.0158798;r <= 0.204011;r+=0.0002)
	{
		SimpsonsApproximation sp(0.0158797, r, funcneg25);
		//cout << r << "\t" << funcneg25(r) << endl;
		theta = sp.calculate(0.00001);

		for (int i =0;i<18;i+=2)
		{
			cout << r*cos(i*thetaN + theta) << "\t" << r*sin(i*thetaN + theta) <<endl;
			cout << r*cos((i+2)*thetaN-theta) << "\t" << r*sin((i+2)*thetaN-theta)  << endl;
		}
	}

	return 0;
}

GNUplot script file:

simpsonsplot.txt