Answer for Final Exam Part 2

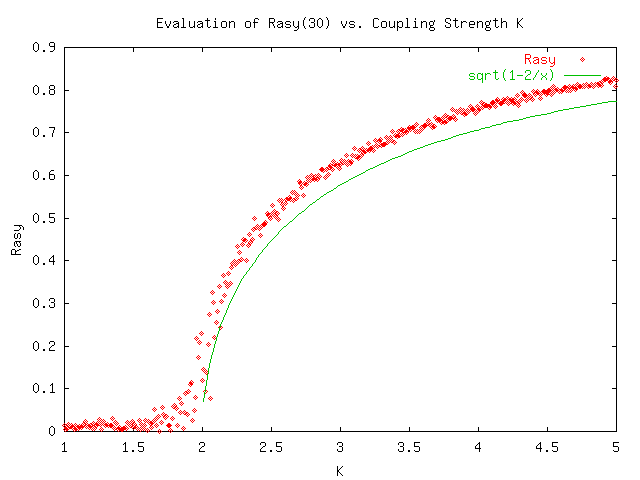
The critical coupling strength was estimated by examining the plot of Rasy(30) vs K in the graph below.  It was around the expected value of 2.  The shape of the function is compared to sqrt(K-2) and proved to match closely. 

#include <iostream>
#include <math.h>
const int pi = acos(-1);

int main(int argc, char* argv[])
{
	const double K_MIN = 1;
	const double K_MAX =5;
	const double K_INC = 0.01;
	double k;

	const double T_MAX = 30;
	const double T_INC = 0.01;
	double t =0;
	double h = T_INC;
	double h2= h/2, h6 = h/6;

	double sinV, cosV;

	const int N = 10000;
	const int w0 = 2;
	int i;

	double w[N], theta_rand[N], theta[N], dydt[N], thetaMid[N], thetaMidDeriv[N], thetaMidDeriv2[N], theta1Deriv[N];
	

	for (k = K_MIN; k < K_MAX; k+=K_INC)
	{
		double r, psi=0;
		double kr = k*r;
		t = 0;

		//generate lorentzian distribution for initial omega's
		//and set the initial phase's to be a random distribution form 0 to 2pi
		//calculate the inital time derivative of theta (dydt)
		for (i = 0; i < N; i++)
		{
			//cout << i << "\t" << 2+ tan(pi*(((double)rand())/RAND_MAX - 0.5)) << endl; 
			w[i] = w0+ tan(pi*(((double)rand())/RAND_MAX - 0.5)) ;
			theta[i] = 2*pi*(((double)rand())/RAND_MAX);
		}

		//perform rk4 approximation 
		do
		{
			//calculate the mean radius and angle of the oscillators
			for (i=0, psi=0, sinV=0, cosV=0;i<N;i++)
			{
				psi += theta[i];
				sinV += sin(theta[i]);
				cosV += cos(theta[i]);
			}
			r = sqrt(sinV*sinV + cosV*cosV)/N;
			psi /= N;

			kr = k*r;

			//estimate theta at time t+h/2 from derivative at time t
			for (i=0; i < N; i++)
			{
				//calculate initial dydt (y = theta)
				dydt[i] = w[i] + kr*sin(psi - theta[i]);

				//calculate theta at the midpoint using initial dydt
				thetaMid[i] = theta[i] + h2*dydt[i];
				//calculate derivative at time t+h/2
				thetaMidDeriv[i] =  w[i] +kr*sin(psi-thetaMid[i]);

				//calculate 2nd thetaMid from thetaMidDeriv
				thetaMid[i] = theta[i] + h2*thetaMidDeriv[i];
				//calculate new thetaMidDeriv using thetaMid calculated by first approximation at time t+h/2
				thetaMidDeriv2[i] =  w[i] + kr*sin(psi - thetaMid[i]);

				//calculate final theta at t+h using 2nd thetaMidDeriv2
				thetaMid[i] = theta[i] + h*thetaMidDeriv2[i];
				//calculate derivative at time t+h
				theta1Deriv[i] =  w[i] + kr*sin(psi - thetaMid[i]);
			

				//use rk4 to estimate the final theta using a  linear combination of previous calculations
				theta[i] += h6*(dydt[i] + 2*thetaMidDeriv[i] + 2*thetaMidDeriv2[i] + theta1Deriv[i]);
			}

			//plot the convergence of phase magnitude r versus time for a given k
			//calculate the mean radius of the phase
			//cout << "\t" << k << "\t" << t << "\t" << r << "\t" << psi << endl;

		} while ((t += T_INC) < T_MAX);

		//calculate the mean radius of the phase
		cout << k << "\t" << r << endl;
	}

	return 0;
}