Physics 510

Assignment 2.

Solution

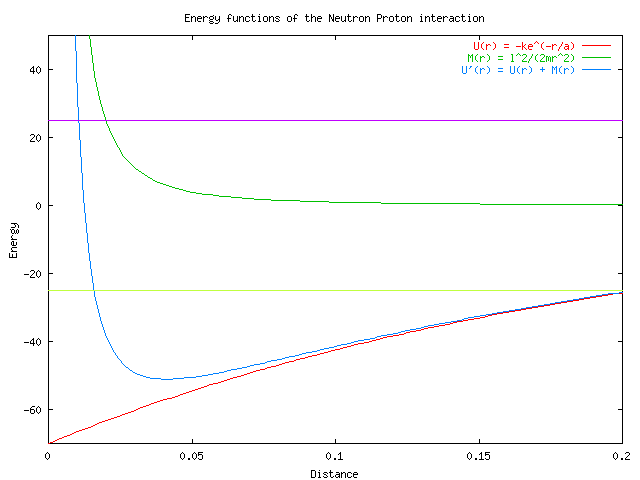
Using GNU plot with the load file newtonsplot.txt produced the following graph which allowed for an educated choice in order to bracket the solutions. 

Where k = 70, a = 0.2, and  l^2/m = 0.01.   The total energy of the system is conserved.  Because we are working in polar coordinates the kinetic energy with respect to the radius is not significant when the particles are either as close together as they come, or as far apart.  At those points dr/dt is zero.  This is also the case at the minimum of the function U'(r), where the two bodies are orbiting one another.   The angular momentum term M(r) is used to take into account the energy of the bodies moving in orbit. 

In order to calculate the boundaries of the equation when the total energy is 25, -25 and at a minimum it was necessary to use the Newton Approximation method.  The solution for energy level 25 was bracketed at [0,0.04] in order to guarantee the derivative estimated approximation did not run to infinity. For energy level -25 the closer boundary condition was bracketed at [0,0.04], while the point of greatest distance between the two bodies was bracketed at [0.05,1].  For the minimum, the zero for the derivative of U'(r) was calculated using the Newton Approximation.  This solution was bracketed at [0,0.1]. The condition of the solution ending up outside the brackets was dealt with in the code by using the bisection method instead of Newton's to close in on the solution.  Precision was chosen to be 0 and a maximum limit (3000) was put on the number of iterations to protect against never achieving such precision because of errors incurred through loss of significant digits.    

The output of the Newton Approximation program is:

Welcome to the Newton Approximation Program for the conservative
central force problem between a neutron and a proton where the 
potential is given by -k*e^(-r/a)
For this example l^2/2m=0.01, k=70, a=0.2 

For energy level 25 the zero found is at : 0.010458
For energy level -25 the lower bound is found at : 0.0158796
 while the upper bound is found at :0.204011
The degenerate case in which the two bodies orbit around each other
is found when r = 0.041259 and E = -51.0771

The source code is composed of six classes, Function, Approximation, NeutronProtonFunc, NeutronProtonDerivativeFunc, NPddFunc and NewtonApproximation.  

The Function class defines an object that represents a function that takes a double precision number and returns the double precision number.     This is syntactically accomplished through the use of operator ().  The Function class inherits from the standard library's unary_function template. It also implemented a getDerivative function. Using function objects allowed the reuse of code when it was necessary to perform an approximation on both the NeutronProtonFunc implementation and the NeutronProtonDerivativeFunc.  By encapsulating the derivative classes within the NeutronProtonFunc it was possible to completely abstract them from the main procedure, thus allowing for alternative implementations in order to retrieve the derivative. 

The Approximation class defines an object that represents an approximation of the function.  It contains a calculate function that takes a precision value and a maximum number of tries.  In future releases it will be possible to implement various approximation functions using this as a base class.  For this example we implemented the NewtonApproximation which was used to find zeros of the NeutronProtonFunc as well as its  minimum value calculated by finding the zeros of the derivative of NeutronProtonFunc.

newtons.cc

#include <functional>
#include <iostream>
#include <math.h>

using namespace std;

class Function : public unary_function<double,double>
{
public:
	Function() {};
	virtual result_type operator()(argument_type x){return x;};
	virtual Function& getDerivative() { return *this;};
};

class ProtonNeutronFunc : public Function
{
public:
	ProtonNeutronFunc(double factor, double exponent_factor, 
		double angular, double energy) 
		:k(factor), a(exponent_factor), m(angular), E(energy), d(factor,exponent_factor,angular) 
	{};

	virtual result_type operator()(argument_type x)
	{
		return -1*k*exp(-1*x/a) + m/pow(x,2) - E;
	};

	virtual Function& getDerivative()
	{
		return d;
	};

protected:
	double k;
	double a;
	double m;
	double E;

	class ProtonNeutronDerivativeFunc : public Function
	{
	public:
		ProtonNeutronDerivativeFunc(double _k, double _a, double _m)
			:	k(_k),a(_a),m(_m), d(_k,_a,_m)
		{};
		result_type operator () (argument_type x) 
		{
			return (k/a)*exp(-1*x/a) - m*2/pow(x,3);
		};
		Function& getDerivative()
		{
			return d;
		};
	protected: 
		class PNddFunc: public Function
		{
		public:
			PNddFunc(double _k, double _a, double _m)
				:	k(_k),a(_a),m(_m)
			{};
			result_type operator () (argument_type x) 
			{
				return m*6/pow(x,4) - (k/pow(a,2))*exp(-1*x/a);
			};
		protected:
			double k;
			double a;
			double m;
		};
	protected:
		double k;
		double a;
		double m;
		PNddFunc d; 
	};
	

	ProtonNeutronDerivativeFunc d;
};

class Approximation
{
public:
	Approximation(double lowerBound, double upperBound, Function& function)
		:a(lowerBound), b(upperBound), f(function)
	{};

	virtual double calculate(double precision, int maxTries = 3000)
	{
		cout << "Default approximation not implemented" << endl;
		return -1;
	}

protected:
	double a;
	double b;
	Function& f;
};

class NewtonApproximation : public Approximation
{
public:
	NewtonApproximation(double lower, double upper, Function& f, Function& derivative)
		:Approximation(lower,upper,f), d(derivative)
	{};
	double calculate(double precision=0.0, int maxTries=3000)
	{
		double x0 = (a+b)/2;
		double xn;
		double p = b-a;
		while ((p > precision) && (--maxTries))
		{
			//cout << "x=" << x0 << "\tf=" << f(x0) <<"\td=" << d(x0) << endl;
			xn = x0 - f(x0)/d(x0);
			if (xn>b) xn = (x0+b)/2;
			if (xn<a) xn = (x0+a)/2;
			p = fabs(x0-xn);
			x0=xn;
			//cout << p << endl;
			

		}
		return xn;
	};
protected:
	Function& d;
};

int main(int argc, char* argv[])
{   
	double r;
	ProtonNeutronFunc func(70, 0.2, 0.01, 0);
	ProtonNeutronFunc func25(70, 0.2, 0.01, 25);
	ProtonNeutronFunc funcneg25(70, 0.2, 0.01, -25);

	cout << "Welcome to the Newton Approximation Program for the conservative" << endl;
	cout << "central force problem between a neutron and a proton where the " <<endl ;
	cout << "potential is given by -k*e^(-r/a)" << endl;
	cout << "For this example l^2/2m=0.01, k=70, a=0.2 " <<endl;
	cout << endl;

	NewtonApproximation newton25(0,0.04,func25, func25.getDerivative());
	cout << "For energy level 25 the zero found is at : " 
		<< newton25.calculate(0.00000001) <<endl;

	NewtonApproximation newtonneg25lower(0,0.04,funcneg25, func25.getDerivative());
	NewtonApproximation newtonneg25upper(0.05,1,funcneg25, func25.getDerivative());
	cout << "For energy level -25 the lower bound is found at : "
		<< newtonneg25lower.calculate(0) <<  endl
		<< " while the upper bound is found at :"
		<< newtonneg25upper.calculate(0) << endl;

	NewtonApproximation newtonmin(0,0.1, func.getDerivative(), func.getDerivative().getDerivative());
	cout << "The degenerate case in which the two bodies orbit around each other" << endl;
	cout << "is found when r = " << (r=newtonmin.calculate());
	cout << " and E = " << func(r) << endl;

	return 0;
};