Answer for Problem 3.1
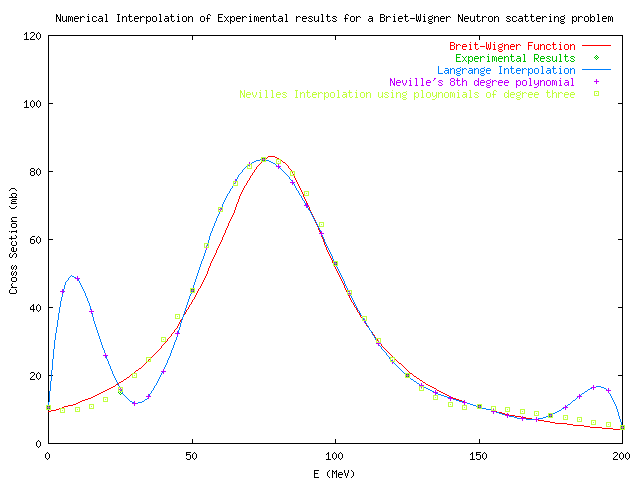
The plot below shows the function representing the cross section for a neutron beam scattering experiment which measures the cross section of the scattering for a neutron beam of a given energy blasts it's nucleus. Using the data given, a standard Neville Interpolation was performed on the data, as well as a Lagrange Interpolation 9th order polynomial, and the most successful of the algorithms, Neville's Interpolation using polynomials of degree three to achieve LOCAL curve fitting.

Data was generated using nevilles.cpp. This file contains a simple recursive function to calculate the value of a function at a given x using data points to interpolate a value at that x. As can be seen from the graph, The 8th order polynomial that was evaluated in the first loop gave some very large deviations from the actual Breit-Wigner curve. The second loop was designed to use only three points at a time to interpolate the polynomial. This gave a much closer fit. It was shown that higher order polynomials introduce inaccuracy into an interpolation.
It is obvious from the graph that using third degree polynomials reduced the error in the interpolation. These points were used to determine the resonant energy and the width of the resonance peak at half height by averaging the solutions of the simultaneous equations given by our interpolated points. The Breit-Wagner function is given as:
cross section= initial cross section / ( ( energy of incoming beam-energy of the resonance ) ^ 2 + resonance width ^ 2 / 4 )
Where initial cross section is assumed to be 6.389x104. Although the actual equation gave the values Energy of resonance = 78, and resonance width = 55, the technique used (averaging out of solution to simultaneous equations) gave values of 85.1348 for the energy of resonance and 63.9752 for the width at half height of the resonance process. In order to verify the algorithm, the solution was bracketed around the peak. This brought the average values much closer to the desired result. At the extremes of the function there is very little change, and insignificant error could sway the solutions to simultaneous equations. Potentially a Monte Carlo, or least squares method might be useful in place of the arithmetic mean. Many of the simultaneous equations derived from the interpolated data did not have a solution. These terms needed to be dropped. The equation is given below.
resonance width = sqrt ( initial cross section / cross section - (energy of beam - energy of resonance) ^2) )
energy of resonance = 1/2 * ( (initial cross section) * (1 / cross section ( i ) - 1 / cross section( i + 1)) - (energy of beam ( i ) ^ 2 + energy of beam ( i + 1 ) ^ 2 ) ) / (energy of beam ( i+1 ) + energy of beam ( i ) )
g(x)=10.6*((x-25)/-25)*((x-50)/-50)*((x-75)/-75)*((x-100)/-100)*((x-125)/-125)*((x-150)/-150)*((x-175)/-175)*((x-200)/-200)\ + 16*((x)/25)*((x-50)/(25-50))*((x-75)/(25-75))*((x-100)/(25-100))*((x-125)/(25-125))*((x-150)/(25-150))*((x-175)/(25-175))*((x-200)/(25-200))\ + 45*(x/50)*((x-25)/(50-25))*((x-75)/(50-75))*((x-100)/(50-100))*((x-125)/(50-125))*((x-150)/(50-150))*((x-175)/(50-175))*((x-200)/(50-200))\ + 83.5*(x/75)*((x-25)/(75-25))*((x-50)/(75-50))*((x-100)/(75-100))*((x-125)/(75-125))*((x-150)/(75-150))*((x-175)/(75-175))*((x-200)/(75-200))\ + 52.8*(x/100)*((x-25)/(100-25))*((x-50)/(100-50))*((x-75)/(100-75))*((x-125)/(100-125))*((x-150)/(100-150))*((x-175)/(100-175))*((x-200)/(100-200))\ + 19.9*(x/125)*((x-25)/(125-25))*((x-50)/(125-50))*((x-75)/(125-75))*((x-100)/(125-100))*((x-150)/(125-150))*((x-175)/(125-175))*((x-200)/(125-200))\ + 10.8*(x/150)*((x-25)/(150-25))*((x-50)/(150-50))*((x-75)/(150-75))*((x-100)/(150-100))*((x-125)/(150-125))*((x-175)/(150-175))*((x-200)/(150-200))\ + 8.25*(x/175)*((x-25)/(175-25))*((x-50)/(175-50))*((x-75)/(175-75))*((x-100)/(175-100))*((x-125)/(175-125))*((x-150)/(175-150))*((x-200)/(175-200))\ + 4.7*(x/200)*((x-25)/(200-25))*((x-50)/(200-50))*((x-75)/(200-75))*((x-100)/(200-100))*((x-125)/(200-125))*((x-150)/(200-150))*((x-175)/(200-175))
set xlabel "E (MeV)" set ylabel "Cross Section (mb)" set title "Numerical Interpolation of Experimental results for a Briet-Wigner Neutron scattering problem" plot [x=0:200] [0:120] 63890/((x - 78)*(x-78) + 55*55/4) title "Breit-Wigner Function", "interdata.txt" using 1:2 title "Experimental Results", g(x) title "Langrange Interpolation", "nevillesdata.txt" every :::0::0 using 1:2 title "Neville's 8th degree polynomial", "nevillesdata.txt" every :::1::1 using 1:2 title "Nevilles Interpolation using ploynomials of degree three"
nevilles.cpp
#include <iostream.h> #include <math.h>
double nevilles(double x, double *data, double * f, int lower, int upper)
{
int a=lower-1;
int b=upper-1;
//cout << a << "," << b << endl;
if (a==b) return f[a];
return (x-data[b])/(data[a]-data[b]) *nevilles(x, data, f, lower, upper-1) +
(x-data[a])/(data[b]-data[a]) *nevilles(x, data, f, lower+1, upper);
}
int main (int argc,char* argv[])
{
const int num_of_values = 9;
double data[num_of_values] = {0,25,50,75, 100,125,150,175,200};
double values[num_of_values] = {10.6, 16.0, 45.0, 83.5, 52.8, 19.9, 10.8, 8.25, 4.7};
int inc =3;
int i, j, k,m;
double x, y, average_x=0, average_y=0;
//double x ;
//while (1)
//{
cout << "# Welcome to the Nevilles Interpolation Alogrithm program" << endl;
//cout << "# These are the data points" << endl;
//for (int i=0;i<num_of_values;i++)
// cout << "# " << data[i] << "\t" << values[i] << endl;
//cout << "# Please enter an x value to interpolate : ";
//cin >> x;
//cout << "# The nevilles algorithm interpolated value is " << nevilles(x, data, values, 1, num_of_values) << endl;
//}
for (i = 0; i <= 200; i+=5) cout << i << "\t" << nevilles(i, data, values, 1, num_of_values) << endl;
cout << endl;
for (i=0, j = inc, k=0,m=0 ;i <= 200; i+=5, k++,m++)
{
cout << i << "\t" << nevilles(i, data, values, j -inc+1, j) << endl;
if (i >= data[j-1] ) j+=inc-1;
}
for (i=0, j = inc, k=0;i <= 200; i+=5)
{
double value = nevilles(i, data, values, j -inc+1, j);
for (int i2=i+5, j2 = j; ((i2 <= 200) && (j2<=num_of_values)); i2+=5)
{
double inner_value = nevilles(i2, data, values, j2 -inc+1, j2);
x = (63890*(1/value - 1/inner_value) - (i)*(i) +i2*i2)/(2*(i2-i));
if ((63890/value - (x-i)*(x-i)) > 0)
{
y = 2*sqrt(63890/value - (x-i)*(x-i));
average_x += x;
average_y += y;
k++;
//cout << x << "\t" << y << endl;
}
if (i2 >=data[j2-1]) j2+=inc-1;
}
if (i >= data[j-1] ) j+=inc-1;
}
cout << "# Average Energy : " << average_x/(k) << endl; cout << "# Average cross section: " << average_y/(k) << endl;
return 0; }
# Welcome to the Nevilles Interpolation Alogrithm program 0 10.6 5 44.8336 10 48.581 15 38.7101 20 25.8487 25 16 30 11.8688 35 13.9312 40 21.2793 45 32.269 50 45 55 57.6522 60 68.7035 65 77.0495 70 82.0473 75 83.5 80 81.5988 85 76.8384 90 69.9177 95 61.6368 100 52.8 105 44.1324 110 36.2148 115 29.442 120 24.0052 125 19.9 130 16.9565 135 14.8904 140 13.3677 145 12.0769 150 10.8 155 9.47062 160 8.2075 165 7.30863 170 7.18987 175 8.25 180 10.6424 185 13.9317 190 16.6117 195 15.4598 200 4.7
0 10.6 5 9.792 10 9.928 15 11.008 20 13.032 25 16 30 19.912 35 24.768 40 30.568 45 37.312 50 45 55 58.236 60 68.704 65 76.404 70 81.336 75 83.5 80 82.896 85 79.524 90 73.384 95 64.476 100 52.8 105 44.316 110 36.784 115 30.204 120 24.576 125 19.9 130 16.176 135 13.404 140 11.584 145 10.716 150 10.8 155 10.37 160 9.9 165 9.39 170 8.84 175 8.25 180 7.62 185 6.95 190 6.24 195 5.49 200 4.7 # Average Energy : 85.1348 # Average cross section: 63.9752