Abdul Khan

Physics 510

George Mason University

Solution to problem 1.2.

In order to solve this problem the algorithm developed for N choose x needed to be protected from loss of significant digits in the overflow of the N!/((x!)(N-x)!)) term.  This was done by using the log(k!) = log ((k-1)!) + log k,  and the series was summed and subtracted concurrently for the three terms making up the choose formula.  The output is plotted below.  In order to further account for precision errors it would be possible to use the following code:

int a = x;
int b = N-x;
int k = 0;
double c = 0;
int sub_total=0;
if (a>b) swap(a,b);

for (int i=b+1;i<=N;i++) 
{
   int lower_terms = 0;
   while ((sub_total<c) && (k<a))
   { 
       k++;
       sub_total += log(k);
       lower_terms += log(k);
    }

    c += log(i) - lower_terms;
}

return pow(exp(1),c);

This was not necessary for this example.  Further tests need to be run to determine performance. 

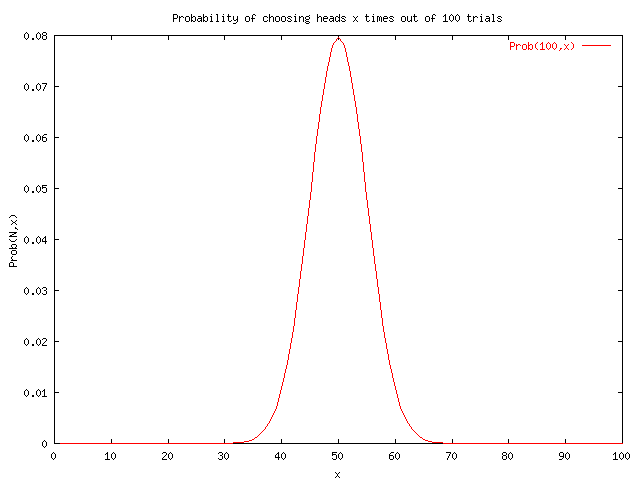
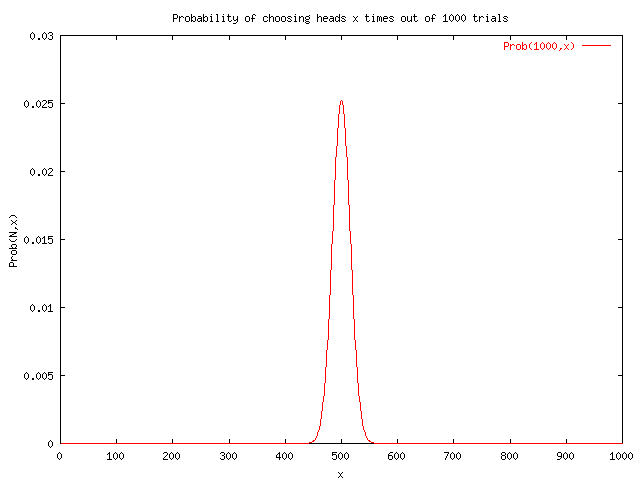
A program probability.cc was written to figure out the probability obtaining x heads in N trials.  This allowed for the calculation of obtaining 30 heads in 100 trials to be  2.31707e-05 and the probability of obtaining 400 heads in 1000 trails to be 4.63391e-11.

The following plots were generated by running the data output of binomial.cc into data files binomial100.txt and binomial1000.txt then using the GNU plot file binomialplot.txt.

// binomial.cpp
//
// Abdul Khan
//

#include <iostream.h>
#include <math.h>

double choose(const double N, const double x)
{
        double c = 0;
        for (int i=1;i<=N;i++)
        {
                c += log(i);
                if (i <= x ) c -= log(i);
                if (i <= N-x) c -= log(i);
        }
        return pow(exp(1),c);
};

int main(int argc, char* argv[])
{
        double N,x;

        double p = 0.5;

        cout << "# This program will calculate the probability that an N \n";
        cout << "# events will result in one of the outcomes exactly x times\n";
        cout << "# for 0<=x<=N";
        cout << "# Please enter N ";
        cin >> N;
        for ( x=0;x<=N;x++)
                cout << x << "\t" << (choose(N,x)*pow(p,x)*(pow((1-p),(N-x)))) << endl;

        return 0;
}

// probability.cpp
//
// Abdul Khan
// 01/30/02
//
// Find the probability that a given even will occur x times in N trials
// Test case returned Prob(100,30)= 2.31707e-05 and Prob(1000,400)= 4.63391e-11

//#include "stdafx.h"
#include <iostream.h>
#include <math.h>

double choose(const double N, const double x)
{
        double c = 0;
        for (int i=1;i<=N;i++)
        {
                c += log(i);
                if (i <= x ) c -= log(i);
                if (i <= N-x) c -= log(i);
        }
        return pow(exp(1),c);
};

int main(int argc, char* argv[])
{
        double N,x;

        double p = 0.5;

        do {
        cout << "This program will calculate the probability that an N evenly chanced\n";
        cout << "events will result in one of the outcomes exactly x times\n";
        cout << "Please enter N ";
        cin >> N;
        cout << "Please enter x ";
        cin >> x;
        cout << "The chances of that are " << (choose(N,x)*pow(p,x)*(pow((1-p),(N-x)))) << endl;
    } while (x && N);

return 0;
};